Diskussionen rund um das Thema "Kombinationen" sind im Poker keine Seltenheit und lassen sich bis ins kleinste Detail vertiefen.
In diesem Überblick reden wir über verschiedene Facetten von Poker Kombinationen und erklären dir, wir du dein strategisches Verständnis vom Spiel verbessern kannst.
- Was ist eine Kombination?
- Hand-Kombinationen im Poker
- Kombinationen in Hold'em berechnen
- Übungsfragen mit Kombis
- Kombinationen und Mathematik
Was ist eine Kombination?
Es gibt zwei leicht unterschiedliche Themengebiete mit demselben Namen.
Die Definitionen:
Kombinationen – Bedeutung
1. Ein singulärer Fall einer bestimmten Pokerhand (normalerweise bezieht sich dies auf die Hole Cards).
2. Mathematik. Eine Auswahl von Gegenständen einer Sammlung, in der es nicht auf die Reihenfolge ankommt.
Mit der mathematischen Definition werden wir uns später nochmals beschäftigen.
Zunächst konzentrieren wir uns auf die erste Definition, die im Zusammenhang mit einer Diskussion im Poker besonders häufig gebraucht wird.
Hand-Kombinationen im Poker
Der Begriff "Kombinationen" (oder Kurzform "Kombi") bezieht sich auf die unterschiedlichen Möglichkeiten, wie sich eine bestimmte Pokerhand zusammensetzen lässt.
Beispiel: In Hold'em erhalten wir Preflop die Hand AK. Wie viele unterschiedliche Kombinationen AK gibt es?
Falls notwendig, könnte man natürlich eine Liste aller möglichen Zusammensetzungen von AK anfertigen. Die meisten Pokerspieler haben sich aber fest eingeprägt, dass es 16 Kombinationen jeder ungepaarten Hand gibt - 12 sind offsuit, 4 sind suited.
Beispiel: In Hold'em erhalten wir Preflop die Hand 66. Wie viele unterschiedliche Kombinationen 66 gibt es?
Auch hier könnten wir alle Kombinationen von 66 auflisten, aber es ist viel einfacher, wenn man verinnerlicht, dass es 6 Kombinationen jedes Pocket Pairs in Hold’em gibt.
1. Ungepaarte Hand - 16 Preflop-Kombis
2. Ungepaarte Offsuit-Hand - 12 Preflop-Kombis
3. Ungepaarte Suited-Hand - 4 Preflop-Kombis
4. Pocket Pair - 6 Preflop-Kombis
Kombinationen in Hold'em berechnen
Es ist relativ einfach, sich an die Preflop Kombis zu erinnern, aber wir müssen auch einberechnen, dass einige Karten aus dem Deck verschwinden und jetzt wird es komplizierter (verschiedene Board-Karten werden bekannt und damit reduzieren sich die verfügbaren Kombinationen von verschiedenen Starthand-Typen).
Hilfreich ist dabei ein System, um Kombis zu berechnen.
Beginnen wir mit den ungepaarten Händen.
Kombis von ungepaarten Händen:
Karte 1: Anzahl der verfügbaren Karten * Karte 2: Anzahl der verfügbaren Karten
Kehren wir kurz zur unserem AK Preflop zurück, können wir jetzt sehen, wie unser Wert von 16 berechnet wurde.
In einem Standard-Deck gibt es 4 Asse und 4 Könige.
Also: 4 * 4 = insgesamt 16 Kombinationen AK
Schwieriger wird es, wenn wir den Effekt der Karten-Entfernung mit einberechnen.
Beispiel: In Hold’em haben wir eine Flop-Textur von Ac8d7h. Wie viele Kombinationen AK gibt es?
Jetzt muss man verstehen, dass sich nur noch 3 Asse im Deck befinden können, da eines davon auf dem Flop liegt. Also gehen wir von 3 verfügbaren Assen und 4 verfügbaren Königen aus.
Also: 3 * 4 = 12 Kombinationen von AK insgesamt.
Nun lernen wir die Regel für Pocket Pairs.
Kombinationen von ungepaarten Händen:
Anzahl der verfügbaren Karten * (Anzahl der verfügbaren Karten - 1)
------------------------------------------------------
2
Kehren wir kurz zu der Preflop-Frage mit der Starthand 66 zurück: Es gibt vier verfügbare Sechser im Deck.
Also: (4 * 3) / 2 = 6 Kombinationen von 66.
Nun eine etwas schwierigere Frage mit der Einberechnung des Effekts der Karten-Entfernung.
Beispiel: In Hold’em haben wir einen Flop von Ac6d7h. Wie viele Kombinationen von 66 gibt es?
Eine 6 liegt bereits auf dem Board, also sind nur noch drei Sechser im Deck übrig.
Also: (3 * 2) / 2 = 3 Kombinationen von 66.
Übungsfragen mit Kombis

Jetzt sollten wir in der Lage sein, etwas kompliziertere Berechnungen in Bezug auf Kombinationen anzustellen. Wir brauchen dazu elementare Rechenkunst und ein wenig gesunden Menschenverstand.
Beispiel: Wir haben vor dem Flop AA bekommen. Wie viele Kombinationen von QQ+/AK kann unser Gegner haben?
Wenn wir den Effekt der Karten-Entfernung kurz ignorieren, wissen wir, dass unser Gegner folgende Kombinationen haben kann:
QQ+ = 18 Kombis (6*3)
AK = 16 Kombis
- macht insgesamt 34 Kombis.
Allerdings haben wir zwei der Asse, also wird die Anzahl der Kombinationen vom Effekt der Karten-Entfernung beeinträchtigt. Dieses Szenario wird manchmal auch als "Blocker-Effekt" beschrieben. Die QQ- und KK-Kombinationen bleiben bei je 6 Kombinationen, aber die AA- und AK-Kombis sind betroffen.
Es gibt 1 Kombi von Assen übrig, da wir die beiden anderen Asse haben.
(2 * 1) / 2 = 1 Kombi Asse
Es gibt 8 Kombis von AK (denn es sind 2 Asse und 4 Könige noch verfügbar)
4 * 2 = 8 Kombis AK
Wenn wir alle Komibs auflisten, erhalten wir folgendes Bild:
AA – 1 Kombi
KK – 6 Kombis
QQ – 6 Kombis
AK – 8 Kombis
macht insgesamt 21 Kombis.
Dies stellt einen bedeutenden Unterschied hinsichtlich der verfügbaren Kombis aufgrund der Karten-Entfernung oder dem "Blocker"-Effekt dar.
Beispiel: In Hold’em haben wir einen Flop von Ac8d7h. Wie viele unterschiedliche Wege gibt es, ein Set zu treffen?
Allgemein sollte man wissen, dass e simmer 3 unterschiedliche Kombinationen von jedem Set gibt. Also haben wir hier 9 Set-Kombinationen.
Versuchen wir, etwas tiefer einzutauchen.
Beispiel: In Hold’em lautet der Flop Ac8d7h. Wie viele unterschiedliche Wege gibt es, Top-Paar zu treffen?
In dieser Situation kommen Logik und gesunder Menschenverstand ins Spiel. Wir wissen, dass es 12 Kombis von allen individuellen Top-Paar-Händen gibt, wie etwa AJ (4 * 3 = 12).
Aber wie viele unterschiedliche Ax-Hände gibt es, die Top-Paar treffen?
Es gibt 13 Karten-Typen im Deck. Wenn wir also AA, A8 und A9 herausnehmen, bleiben 10 unterschiedliche Typen von Ax-Händen, mit denen Top-Paar möglich ist. Jede hat 12 Kombinationen. Also gibt es 120 (10 * 12) verschiedene Kombinationen von Top-Paar auf dieser Textur.
Dabei handelt es sich weiterhin um eine recht einfache Berechnung. Es wird aber noch komplexer. Zum Glück gibt es Equity Rechner auf dem Markt, die uns in komplexen Situationen genau zeigen können, wie viele Kombinationen es gibt.
Kombinationen und Mathematik
Jetzt widmen wir uns der zweiten Definition des Begriffs Kombinationen.
Mathematik: Eine Auswahl von Gegenständen einer Sammlung, in der es nicht auf die Reihenfolge ankommt.
Bis jetzt haben wir gelernt, wie man Hole Card Kombinationen berechnet. Diese zweite Definition hilft uns, die Wahrscheinlichkeit von verschiedenen Board-Runouts (zukünftige Straßen bis zum River) zu berechnen.
Schreiben wir unsere Definition um, damit sie für Poker relevant wird.
Poker: Eine Auswahl von Karten aus dem Deck, für die eine Anordnung keine Bedeutung hat.
Beginnen wir mit einer Beispiel-Frage.
Oft heißt es, dass 19.600 unterschiedliche Flops in Hold'em möglich sind. Wir demonstrieren dies auf mathematischer Weise mithilfe von Kombinationen.
Beginnen wir mit der mathematischen Formel für Kombinationen.
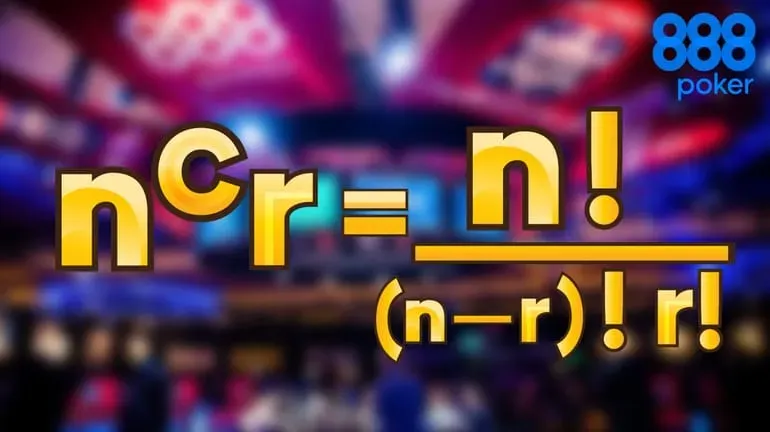
Definieren wir die Werte der Formel.
n = Gesamtzahl, von der man aussucht (also die Anzahl der Karten im Deck)
r = Gesamtzahl, die wir aussuchen (also wie viele Karten wir aus dem Deck entnehmen)
C = Kombinationen
! = mathematische Funktion bekannt als "faktoriell" (Beispiel: 5! Es ist 5 * 4 *3 *2 *1)
Teilen wir n und r Werte zu.
n = 52, weil es 52 Karten im Deck gibt
r = 3, weil wir 3 Karten aus dem Deck für den Flop brauchen.
Jetzt werfen wir alle Zahlen in die Formel hinein -
52!
-----
(49!) * 3!
Es ist möglich, diese Zahlen direkt in einen Taschenrechner einzutippen (mithilfe der richtigen Klammern), aber es ist auch möglich, die Formel manuell zu vereinfachen.
Die Vereinfachung zielt etwas über die Absicht dieses Artikels hinaus, aber sie ist nicht zu kompliziert.
52 * 51 * 50
-----------------
6
Ergebnis: Es gibt 22.100 verschiedene Flop-Kombinationen. Interessant. Warum sagt uns die Online-Suchmaschine, dass es 19.600 Flop-Kombinationen gibt= Liegt es daran, dass diese Berechnungen davon ausgehen, dass 2 Karten im Deck bereits bekannt sind (unsere Hole Cards)?
Starten wir mit der Berechnung neu.
n = 50, weil es noch 50 Karten gibt, nachdem wir unsere Hole Cards erhalten haben.
r = 3, weil wir 3 Karten aus dem Deck für den Flop brauchen.
Dieses Mal erhalten wir –
50!
-----
47! * 3!
Vereinfacht:
50 * 49 * 48
------------------
6
- ergibt 19.600!
Wenn jemand behauptet, dass es 19.600 Flops gibt, dann bedeutet es, dass 2 Karten vom Deck bereits bekannt sind. Wir haben gelernt, dass es 22.100 verschiedene Flops gibt, die ein Außenstehender erwarten kann (gesetzt den Fall, dass er keine der Hole Cards kennt).
Nutzen wir unsere neuen Kenntnisse über Kombinationen, um eine etwas schwierigere Frage zu beantworten.
Beispiele: Wir erhalten ThJh in Hold’em. Wie stehen unsere Chancen, einen Flush zu floppen?
Wir wissen bereits, wie viele Flops es gibt (19.600), also muss unser nächstes Ziel sein, herauszufinden, wie viele Wege es gibt, einen Herz-Flush zu floppen, wenn wir von elf verbleibenden Herzen im Deck ausgehen.
Wie können wir die Anzahl der verschiedenen 3-Karten-Kombinationen bestimmen, die aus einer Auswahl von elf Karten gedealt werden können?
Diese Kalkulation ist genau dies, wofür es mathematische Kombinationen gibt.
n = 11, weil dies die Anzahl der Herzen darstellt, die im Deck verbleiben (gesetzt den Fall, dass wir 2 Herzen auf der Hand haben).
r = 3, weil wir 3 Karten aus dem Deck für den Flop brauchen..
Ab mit den Zahlen in unsere Formel –
11!
----------
8! * 3!
- vereinfacht ausgedrückt
11 * 10* 9
---------------
6
= 165 Wege, die zu 3 Herzen auf dem Flop führen.
Die Wahrscheinlichkeit, dass wir 3 Herzen auf dem Flop bekommen, liegt also bei:
165 / 19,600 = 0.0084 oder 0.84%
Wenn wir allerdings mit dem Equity-Rechner nachprüfen, sagt uns dieser, dass die Chance auf einen gefloppten Flush bei 0,82 Prozent und nicht bei 0,84 Prozent liegt. Weißt du, warum e seine Diskrepanz gibt?
Einige der Flops mit drei Herzen geben uns einen Straight Flush. Wir müssen wissen, wie viele es sind, damit wir diese von unserer Gesamtzahl von Flush-Flops abziehen können.
Flops, die bei einer Starthand von ThJh zu einem Straight Flush führen:
AhKhQh
KhQh9h
Qh8h9h
7h8h9h
Vier unterschiedliche Flops also. Diese ziehen wir jetzt von unserer Gesamtzahl von 165 ab...
161 / 19,600 = 0.0082 oder 0.82%
Voila! Wir sind bei 0,82 Prozent angekommen und können dem Equity-Rechner also weiter Glauben schenken.
Versuchen wir uns an einem weiteren Beispiel.
Beispiel: Wir bekommen AKo, wie stehen unsere Chancen, eine Straße zu basteln?
Vielleicht siehst du ein Muster für die vereinfachte Version der Formel, wenn du Kombinationen nutzt, um die Wahrscheinlichkeit von verschiedenen Flops zu berechnen.
Das Muster geht so:
Anzahl von Karte 1 * Anzahl von Karte 2 * Anzahl von Karte 3
-------------------------------------------------------------------------
3!
Wenn wir also auf eine Straße hoffen, müssen wir unbedingt einen TJQ-Flop haben (die Reihenfolge der Karten ist egal).
Es gibt 12 Wege, um entweder T, J oder Q auf dem Flop zu bekommen.
Es gibt 8 Wege, wie wir J oder Q bekommen, wenn wir davon ausgehen, dass eine T auf dem Flop liegt (unabhängig von der Flop-Karte gibt es 8 Wege, um einen Teil der Straße auf dem Turn zu treffen). Es gibt 4 Wege, wie wir die Straße auf dem River komplettieren.
12 * 8 * 4
---------------
3!
Wenn wir die obere Hälfte der Formel (12 * 8 * 4) multiplizieren, erhalten wir 384. Die Lösung ist die Anzahl der unterschiedlichen Wege, wie man eine Straße floppt, wenn wir davon ausgehen, dass die Reihenfolge der Karte egal ist (was nicht der Fall ist).
Deshalb legt 384 nahe, dass es sich bei TcJhQd und JhTcQd um unterschiedliche Flops handelt. Für den Zweck unserer Rechnung sind sie es aber nicht. Der mathematische Name einer Auswahl, in der die Reihenfolge von Bedeutung ist, lautet Permutation anstatt Kombination und beinhaltet eine etwas unterschiedliche Formel.

Der zweite Teil der Formel (teile durch 3! oder 6) wird benutzt, um Flop-Duplikate (jedoch mit unterschiedlichen Reihenfolgen) zu berechnen.
384
------
6
= 64
Also bleiben uns 64 unterschiedliche Wege, um eine Straße zu erhalten, wenn die Reihenfolge der Flop-Karten keine Bedeutung hat.
Deshalb: 64 / 19600 = 0.003265 oder 0.33%
Um diese Frage zu beantworten, muss man nicht unbedingt Kombinationen nutzen… Wir können die Antwort finden, in dem wir die grundlegende Wahrscheinlichkeits-Formel für die Wahrscheinlichkeit von aufeinanderfolgenden Events nutzen.
Schauen wir mal, wie dies funktioniert:
Aktion 1 – Die erste Flop-Karte ist entweder T, J oder Q = 12/50, weil 50 Karten im Deck verbleiben.
Aktion 2 – Die zweite Flop-Karte ist eine der verbliebenen acht Karten, die wir für eine Straße brauchen = 8/49, weil 49 Karten im Deck verbleiben.
Aktion 3 – Die dritte Flop-Karte ist eine der verbliebenen vier Karten, die wir brauchen, um die Straße zu komplettieren = 4/48, weil 49 Karten im Deck verbleiben.
In der Wahrscheinlichkeitstheorie müssen wir einfach die Wahrscheinlichkeiten von jeder aufeinanderfolgenden Aktion multiplizieren, um die Gesamtwahrscheinlichkeit zu berechnen.
12/50 * 8/49 * 4/48 = 0.003265
Kommt dir diese Zahl bekannt vor? Es ist genau der gleiche Wert, den wir vorhin berechnet haben, wenn wir mit AK eine Straße floppen wollen.
Zusammenfassung: Hand-Kombinationen
Die am meisten benutzte Art von Kombination ist die Hand, die wir ganz am Anfang diskutiert haben. Wir sollten allgemein davon ausgehen, dass ein Spieler darüber diskutieren will, wenn er das Thema Kombinationen auf den Tisch bringt.
Im Kontrast dazu wissen viel weniger Spieler über mathematische Kombinationen Bescheid. Der durchschnittliche Spieler hat davon wahrscheinlich sogar noch nie gehört. Berechnen kann er es eher nicht. Wer sich eine gute Übersicht solcher mathematischen Konzepte verschafft, hat einen großen Vorteil gegenüber dem Rest des Feldes.
Wir haben gelernt, dass es 19.600 unterschiedliche Flops gibt, wenn man seine beiden Hole Cards kennt. Wir können Kombinationen nutzen, um herauszufinden, wie oft bestimmte Typen von Flops kommen und können das Ergebnis durch 19.600 teilen, um die entsprechende Wahrscheinlichkeit herauszufinden.


